Globalization
- Get link
- X
- Other Apps
In my previous post, "Life, Death, and 'The Winner Takes It All'" I discussed a simple differential equation that can be used to calculate population size \begin{equation} \large{}\color{blue}\frac{d x}{d t} = x \end{equation}This equation, known as the exponential function, becomes more complex when it incorporates death rates (the logistic function) and competition (the "struggle of information" model). However, the underlying principle of these models remains the same: the growth rate of a population is proportional to its current size. This principle holds true for most species, but there is one notable exception: humans.
Humans are unique in that their population growth does not follow the basic principle outlined above. The study of human population size and growth rates is known as demography. Demographers collect statistics on the number of people in different areas and develop mathematical models to represent these numbers as accurately as possible. These models can be used to predict future population sizes, which is a crucial piece of information for understanding various economic and political processes. Population size affects the amount of resources that people need and may point to potential problems.
One of the most significant recent demographic studies was conducted by Russian scientist Professor Sergey Kapitsa. His research is summarized in the book "PARADOXES OF GROWTH: LAWS OF GLOBAL DEVELOPMENT OF HUMANITY." Professor Kapitsa was interested in investigating one of the most complex known systems: humanity. He proposed that every complex system has a parameter that has the most significant impact on its behavior. Professor Kapitsa hypothesized that for humanity, this parameter is the global human population size. He collected data on the global human population over time.
 |
| picture from book by Sergey Kapitsa |
There is axis of years and axis of number of people, number of people scale is logarithmic.
Kapitsa's analysis revealed that the growth rate of the human population is proportional to the square of the current global population size. \begin{equation} \large{}\color{blue}\frac{d N}{d T} = \frac{N^2}{2*10^{11}} \end{equation} There are many very interesting conclusions that follow from this
equation and whole research of professor Kapitsa, I'll talk about some
of them in another blog post. Here I want to show one of conclusions
that Kapitsa emphasize.
This finding has important implications for our understanding of human population growth. While this model accurately represents global human population growth over hundreds of thousands of years, it fails to accurately model population growth at the local level. Professor Kapitsa explained it by simple mathematical fact. Growth rate of humanity is proportional to square of current number of people over globe. In case we replace total number of people over globe by sum of people in different areas we cannot say that is those areas population growth is also related to square in area. This is because the square of a sum does not equal the sum of squares. \begin{equation} \Large{}\color{black} (a+b)^2 \neq a^2+b^2 \end{equation} In other words, the population growth of individual local areas cannot be determined by simply adding up the population growths of those areas.
I thought to myself it's funny that there is mathematical expression showing that humanity is understandable only globally and is unpredictable when we try to analyze it locally.
- Get link
- X
- Other Apps
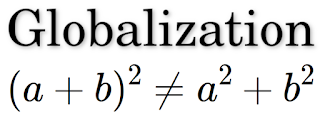

Comments
Post a Comment