"Life", "Death" and "The Winner Takes It All"
- Get link
- X
- Other Apps
I want to talk about how one simple differential equation became very useful mathematical model that reflect how different ecosystems (both in nature and in technology) evolve.
"Life"
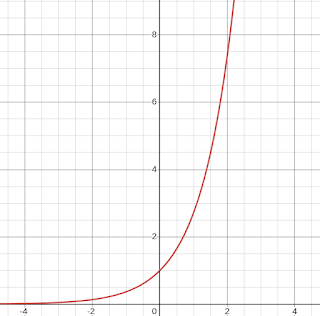
One of most known ecosystems used for mathematical modeling is population of rabbits. We assume that next generation of rabbits will have all already living rabbits plus new born rabbits. Number of new born rabbits is proportional to number of existing rabbits. We'll take simplest case when number of additional rabbits equal to number of existing rabbits (when 2 rabbits bring 2 new rabbits). This means that change of number of rabbits equal to number of rabbits, or as differential equation: \begin{equation} \large{}\color{blue}\frac{d x}{d t} = x \end{equation} General solution for this differential equation is: \begin{equation} \Large{}\color{blue} x = e^t \end{equation}(where X is population number, T is time). This equation is known as "exponential function".
Many times this function used to represent population growth of living elements of system. Living objects are such that can reproduce themself (like rabbits or virus). Living object may be not only "life" elements, but also "non real" elements like piece of information. In case someone reveal some information number of people that "know" this information also will grow exponentially.
Exponential growth is very fast growth, it is often used to express "blowup" growth. While exponential growth used by many to express population growth in reality it's wrong representation. No population grow accordingly exponential function because that growth cannot be infinite. There is another function that more close to describe population growth.
"Death"
Any population has growth limit. When population is small it grows fast because there is almost no death. When population closer to resource limits more species start to die. Original differential equation get "death" element. We assume that death rate proportional to number of species and proportional to relation of number of species to maximum number environment allow. \begin{equation} \large{}\color{blue}\frac{d x}{d t} = x-x*\frac{x}{L} \end{equation} or \begin{equation} \large{}\color{blue}\frac{d x}{d t} = x-\frac{x^2}{L} \end{equation} (L is population maximum limited by environment) When current population significantly smaller than maximum population growth very close to exponential, but when x became close to maximum L death rate became very close to birth rate and makes growth almost 0. General solution to this function is \begin{equation} \large{}\color{blue}x = \frac{L}{1+e^{-t}} \end{equation} This function is known as "logistic function".
This function was introduced by Belgian mathematician Pierre Verhulst. It is used in many domains, from ecology and health to machine learning. This function has "S" shape and is one of "Sigmoid" functions. Logistic function is interesting for TRIZ (Theory of Inventive Problem Solving), because one of TRIZ laws of system evolution is that useful parameters in technical systems grow with S-curve. It's very interesting to apply logistic function on "S-curve" law of TRIZ.
Direct analogy of "logistic function" and "S-curve" is wrong because number of elements of some species in ecological system and number representing some system's parameter (e.g. car speed or screen size of TV) are very different numbers in their nature. But, if we consider that there is correlation between useful parameter and number of subsystems in system and number of relations between subsystems, we can find that such analogy may be possible. What we can say is that "Complexity" of system grows accordingly to "logistic function". Many interesting questions come from it. Is it possible to express "complexity" of technical system mathematically? Why complexity has limit in technical system? (I have some ideas on these issues, but I'll represent them in another blog).
"The Winner Takes It All"
There is one important aspect in population growth that should be considered. Competition. Ecological model where we have only one type of species (e.g. rabbits) is too simplified. In real world resources may be useful for many different species, which leads to direct competition between species. We can express competition in differential equation by adding part that reduce growth rate. Number of differential equations will be equal to number of species in system (one differential equation for each species). Let's see how it looks like for 2 species. \begin{equation} \large{}\color{blue}\frac{d x_{1}}{d t} = x_{1}-a_{1}x_{1}^2-b_{12}x_{1}x_{2} \end{equation} \begin{equation} \large{}\color{blue}\frac{d x_{2}}{d t} = x_{2}-a_{2}x_{2}^2-b_{21}x_{2}x_{1} \end{equation} ("a" is coefficient of internal competition in some of species, "b" is competition coefficient between species). Now we build equation where growth of species "1" depends also on species "2". General form for many information types. \begin{equation} \large{}\color{blue}\frac{d x_{i}}{d t} = x_{i}-a_{i}x_{i}^2-\sum_{j \neq i}^n b_{ij}x_{i}x_{j} \end{equation} This mathematical model was represented by Russian scientist Dmitrii Chernavskii and is called "Struggle of Informations". By "Information" in this model we mean some entity that can reproduce itself. It may be some living species (like virus or rabbit). It may be technological standard, rumors, ... anything that can be replicated. Those informations may coexist and do not affect each other (coefficient "b" is very low), or informations may not coexist ("b" is very high). Informations with high "b" coefficient are called "antagonistic". Accordingly to "Struggle of Information" model when in system there are 2 antagonistic "informations" it leads to "pure" state where only one of two informations will survive, another information will disappear with time. This effect is known as "The winner takes it all". It does not matter that some information has very little advantage over another information, it still will lead to situation that another information will disappear totally.
I'll give an example from technological domain. When mechanical clocks invented part of them had 12 hours and part of them had 24 hours.
Those two types of clock are different in way they represent time, in our words those are two different informations. Lets think, are those informations antagonistic each to other? Lets imagine in some town two men decide to meet tomorrow at 11 o'clock. In case those two men has different types of clock they will not meet. With time all men in this town will have only one type of clock. Clock with 24 hours totally disappeared. It's not that 12 hours clock has very big advantage over 24 hours clock, but because those two types are antagonistic only one will survive.
Another good example of "Struggle of Informations" is relations between programming languages. Programming languages may be antagonistic in case they try to solve similar problems, e.g. many scripting languages are antagonistic each to other. We can see that last years one scripting language usage significantly grow, while other scripting languages used much less than before. Programming languages may be not antagonistic (like "C" and "JavaScript") because they are solve different problems and programmers do not need to select one of them.
Professor Chernavskii used "Struggle of Informations" model to explain why all living forms on our planet use same genetic code. This model can be very useful for understanding process how one of many technologies became standard, while other disappear. This model also used to explain some historical processes where countries were united because languages are antagonistic. This model is also useful in economics, it can be good tool to understand how different currencies behave locally and globally.
- Get link
- X
- Other Apps



Comments
Post a Comment